Spin spirals

Generalized Bloch condition

Spin spirals may be conveniently modeled using a generalization of the Bloch condition (set LNONCOLLINEAR=.TRUE. and LSPIRAL=.TRUE.):

$\left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\ \Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left( \begin{array}{cc} e^{-i\bf q \cdot \bf R / 2} & 0\\ 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right],$

i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of $\exp(-i{\bf q}\cdot {\bf R}/2)$ and $\exp(+i{\bf q}\cdot {\bf R}/2)$, respectively, where R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.

The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the QSPIRAL-tag.

The generalized Bloch condition above gives rise to the following behavior of the magnetization density:

${\bf m} ({\bf r} + {\bf R})= \left( \begin{array}{c} m_x({\bf r}) \cos({\bf q} \cdot {\bf R}) - m_y({\bf r}) \sin({\bf q} \cdot {\bf R}) \\ m_x({\bf r}) \sin({\bf q} \cdot {\bf R}) + m_y({\bf r}) \cos({\bf q} \cdot {\bf R}) \\ m_z({\bf r}) \end{array} \right)$

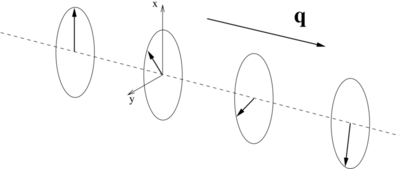
This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.

Basis set considerations

The generalized Bloch condition redefines the Bloch functions as follows:

$\Psi^{\uparrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\uparrow}_{\bf k \bf G} e^{i(\bf k + \bf G -\frac{\bf q}{2})\cdot \bf r}$

$\Psi^{\downarrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\downarrow}_{\bf k \bf G} e^{i(\bf k + \bf G +\frac{\bf q}{2})\cdot \bf r}$

This changes the Hamiltonian only minimally:

$\left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} \\ V^{\downarrow\uparrow}_{\rm xc} & H^{\downarrow\downarrow} \end{array}\right) \rightarrow \left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} e^{-i\bf q \cdot \bf r} \\ V^{\downarrow\uparrow}_{\rm xc}e^{+i\bf q \cdot \bf r} & H^{\downarrow\downarrow} \end{array}\right),$

where in $H^{\uparrow\uparrow}$ and $H^{\downarrow\downarrow}$ the kinetic energy of a plane wave component changes to:

$H^{\uparrow\uparrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} - {\bf q} /2|^2$

$H^{\downarrow\downarrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} + {\bf q} /2|^2$

In the case of spin-spiral calculations the cutoff energy of the basis set of the individual spinor components is specified by means of the ENINI-tag.

Additionally one needs to set ENMAX appropriately: ENMAX needs to be chosen larger than ENINI, and large enough so that the plane wave components of both the up-spinors as well as the components of the down-spinor all have a kinetic energy smaller than ENMAX. This is the case when:

$\mathtt{ENMAX} \geq \frac{\hbar^2}{2m}\left( G_{\rm ini} + |q| \right)^2$

where

$G_{\rm ini}=\sqrt{\frac{2m}{\hbar^2}\mathtt{ENINI}}$

In most cases it is more than sufficient to set ENMAX=ENINI+100.

To judge whether ENMAX is chosen large enough one will always get a warning at runtime, e.g.

 ----------------------------------------------------------------------------- 
|                                                                             |
|           W    W    AA    RRRRR   N    N  II  N    N   GGGG   !!!           |
|           W    W   A  A   R    R  NN   N  II  NN   N  G    G  !!!           |
|           W    W  A    A  R    R  N N  N  II  N N  N  G       !!!           |
|           W WW W  AAAAAA  RRRRR   N  N N  II  N  N N  G  GGG   !            |
|           WW  WW  A    A  R   R   N   NN  II  N   NN  G    G                |
|           W    W  A    A  R    R  N    N  II  N    N   GGGG   !!!           |
|                                                                             |
|      To represent the spin spiral you requested, with a kinetic             |
|      energy cutoff of ENINI=  300.00 eV, choose ENMAX >  331.21 eV          |
|      Currently ENMAX=  400.00 eV                                            |
|                                                                             |
 -----------------------------------------------------------------------------

Symmetry

Generally the spin-spiral lowers the symmetry of the system. At present