Spin spirals

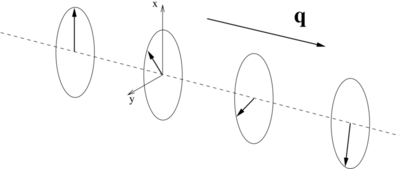
Generalized Bloch condition

Spin spirals may be conveniently modeled using a generalisation of the Bloch condition:

$\left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\ \Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left( \begin{array}{cc} e^{-i\bf q \cdot \bf R / 2} & 0\\ 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right],$

i.e., from one unit cell to the next the up-spinor and down-spinors pick up an additional phase factor of $\exp(-i{\bf q}\cdot {\bf R}/2)$ and $\exp(-i{\bf q}\cdot {\bf R}/2)$, respectively.

The above definition gives rise to the following magnetization density:

${\bf m} ({\bf r} + {\bf R})= \left( \begin{array}{c} m_x({\bf r}) \cos({\bf q} \cdot {\bf R}) - m_y({\bf r}) \sin({\bf q} \cdot {\bf R}) \\ m_x({\bf r}) \sin({\bf q} \cdot {\bf R}) + m_y({\bf r}) \cos({\bf q} \cdot {\bf R}) \\ m_z({\bf r}) \end{array} \right)$

This is schematically depicted in the figure at the top of this page.