Category:Electron-phonon interactions: Difference between revisions
No edit summary |
|||
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
In | In many systems it suffices to treat the [[electronic minimization|electronic]] and [[phonons|vibrational degrees of freedom]] (phonons) separately, because electrons are much faster than the motion of nuclei. This treatment is approximate and can be corrected by including '''electron-phonon coupling'''. This entails the coupling of the two systems, while still treating the two systems separately. In fact, phonon scattering is the prevalent effect in a wide range of applications such as mobility of semiconductors or conductivity of metals at room temperature. | ||
The inclusion of the effects of the ionic degrees of freedom in the electronic structure is important in the determination of many physical observables such as the bandgap, spectral functions, electronic conductivity, Seebeck coefficient or electronic thermal conductivity to name a few. | The inclusion of the effects of the ionic degrees of freedom in the electronic structure is important in the determination of many physical observables such as the [[Bandgap_renormalization_due_to_electron-phonon_coupling|bandgap]], spectral functions, [[:Category:Dielectric properties|electronic conductivity]], Seebeck coefficient or electronic thermal conductivity to name a few. | ||
One can use different approaches to include '''electron-phonon coupling''': | |||
In this page we outline the two later approaches, their advantages and disadvantages and range of application. | * statistically averaging observables during a molecular dynamics calculation, | ||
* [[#Stochastic displacements approach|stochastically sampling the ionic degrees of freedom]], or | |||
* using [[#Many-body perturbation theory|many-body perturbation theory]] (available as of VASP 6.5.0). | |||
In this page we outline the two later approaches, their advantages and disadvantages and range of application. For a comprehensive overview of the theory of electron-phonon coupling, we recommend the review by F. Giustino {{cite|giustino:rmp:2017}}. | |||
== | == Stochastic displacements approach == | ||
The [[Electron-phonon interactions theory#Electron-phonon interactions from statistical sampling|stochastic approach]] allows obtaining the bandgap renormalization and an approximation of the electronic spectral function due to the ionic degrees of freedom under the static approximation using a supercell approach. This has the advantage that it can be easily implemented and used with different levels of theory to describe the electronic states, such as different [[exchange-correlation functionals]] or even the [[:Category:GW|GW approximation]]. The disadvantage is that the approach does not include time-dependent or dynamical effects of the phonons (static approximation) and, hence, it does not provide transport properties (see [[#Many-body perturbation theory|perturbative approach]]). Additionally, it is computationally demanding as it requires many supercell calculations. | |||
The [[Electron-phonon interactions theory| | To displace the atoms along a set of random or a single specially chosen direction {{cite|zacharias:prb:2016}}, this approach requires the knowledge of the [[phonons]] on a supercell. The displacement length is determined by the temperature of the ionic system. The bandgap can be directly obtained by averaging over the set of randomly displaced supercells, or from the aforementioned special displacement pattern. | ||
*[[Electron-phonon interactions from Monte-Carlo sampling]] | |||
== Many-body perturbation theory == | |||
[[File:Elphon-workflow.png|400px|thumb|right|General workflow when running electron-phonon calculations using perturbation theory.]] | |||
Another approach to include '''electron-phonon coupling''' employs the methods and language of many-body perturbation theory, where the coupling is included as a perturbation of the electronic or phononic states. | |||
In the case of the perturbation of the electronic states, we can access the [[Bandgap_renormalization_due_to_electron-phonon_coupling|bandgap renormalization]] as well as [[Transport_coefficients_including_electron-phonon_scattering|electronic transport coefficients]] with the inclusion of phonon scattering. | |||
This approach entails computing the ''electron-phonon matrix element'' and the phonon-induced electron self-energy. Within the framework of density-functional theory this requires the knowledge of the change of Kohn-Sham potential with an ionic perturbation as well as the initial and final electronic Kohn-Sham states. The calculation is done in two steps: | |||
== | === Step 1: [[Electron-phonon potential from supercells]] === | ||
*[[ | :In the first step, we obtain the derivatives of the Kohn-sham potential with respect to the ionic displacements | ||
::<math> | |||
\partial_{I \alpha} V (\mathbf{r}) = \frac{\partial V(r)}{\partial R_{I\alpha}} | |||
</math> | |||
:with <math>I</math> the ion index and <math>\alpha</math> denoting the Cartesian direction in which it is displaced. The main output file is {{FILE|phelel_params.hdf5}}, which is required for computing the matrix elements in the next step. | |||
:* How to compute the [[electron-phonon potential from supercells]] | |||
=== Step 2: Physical observables (or electron-phonon matrix elements) === | |||
:To compute the physical observables, the phonon-induced electron self-energy is computed in the primitive cell. The main tag that provides convenient defaults depending on the observable of interest is {{TAG|ELPH_MODE}}. The computation of the self-energy requires evaluating the electron-phonon matrix elements | |||
::<math> | |||
g_{mn \mathbf{k}, \nu \mathbf{q}} | |||
\equiv | |||
\langle | |||
\psi_{m \mathbf{k} - \mathbf{q}} | | |||
\partial_{\nu \mathbf{q}} V | | |||
\psi_{n \mathbf{k}} | |||
\rangle. | |||
</math> | |||
:By default, we avoid writing the matrix elements, because it is a huge data set which is distributed for optimal use of the computational resources. | |||
*[[ | :For details on the setup and practical advice, we recommend reading | ||
:* [[Bandgap renormalization due to electron-phonon coupling]] | |||
:* [[Transport coefficients including electron-phonon scattering]] | |||
:* See the {{TAG|ELPH_DRIVER}} tag to obtain the electron-phonon matrix elements for further post-processing. | |||
<!----- | |||
==== [[Bandgap renormalization due to electron-phonon coupling]] ==== | |||
The bandgap renormalization is computed from the real part of the Fan-Migdal and Debye Waller contributions to the electron self-energy. | |||
To get an accurate value, we need to carefully consider both basis set (number of plane-waves and KS states) as well as <b>k</b>-points used to evaluate the electron self-energy. | |||
The transport coefficients are computed within the framework of the linearized Boltzmann transport equation, which in turn requires the knowledge of the electronic lifetimes due to every possible scattering event. There are a few approximations for these scattering rates: in the constant-relaxation time approximation (CRTA), an empirical parameter is used to approximate the scattering rate throughout the Brillouin zone | ==== [[Transport coefficients including electron-phonon scattering]] ==== | ||
The transport coefficients are computed within the framework of the linearized Boltzmann transport equation, which in turn requires the knowledge of the electronic lifetimes due to every possible scattering event. There are a few approximations for these scattering rates: | |||
# in the constant-relaxation time approximation (CRTA), an empirical parameter is used to approximate the scattering rate <math>\tau_{n\mathbf{k}} = \tau</math> throughout the Brillouin zone | |||
# in the self-energy relaxation time approximation (SERTA) or energy relaxation time approximation (ERTA), the lifetimes are approximated from the electron self-energy <math>\tau_{n\mathbf{k}} = [2\Sigma_{n\mathbf{k}}(\epsilon_{n\mathbf{k}})]^{-1}</math> | |||
# in the momentum relaxation time approximation (MRTA) an additional geometric factor is included to account for the correct balance between inwards and outwards scattering. | |||
-----> | |||
== References == | |||
<references/> | |||
Latest revision as of 10:17, 5 February 2025
In many systems it suffices to treat the electronic and vibrational degrees of freedom (phonons) separately, because electrons are much faster than the motion of nuclei. This treatment is approximate and can be corrected by including electron-phonon coupling. This entails the coupling of the two systems, while still treating the two systems separately. In fact, phonon scattering is the prevalent effect in a wide range of applications such as mobility of semiconductors or conductivity of metals at room temperature.
The inclusion of the effects of the ionic degrees of freedom in the electronic structure is important in the determination of many physical observables such as the bandgap, spectral functions, electronic conductivity, Seebeck coefficient or electronic thermal conductivity to name a few.
One can use different approaches to include electron-phonon coupling:
- statistically averaging observables during a molecular dynamics calculation,
- stochastically sampling the ionic degrees of freedom, or
- using many-body perturbation theory (available as of VASP 6.5.0).
In this page we outline the two later approaches, their advantages and disadvantages and range of application. For a comprehensive overview of the theory of electron-phonon coupling, we recommend the review by F. Giustino [1].
Stochastic displacements approach
The stochastic approach allows obtaining the bandgap renormalization and an approximation of the electronic spectral function due to the ionic degrees of freedom under the static approximation using a supercell approach. This has the advantage that it can be easily implemented and used with different levels of theory to describe the electronic states, such as different exchange-correlation functionals or even the GW approximation. The disadvantage is that the approach does not include time-dependent or dynamical effects of the phonons (static approximation) and, hence, it does not provide transport properties (see perturbative approach). Additionally, it is computationally demanding as it requires many supercell calculations.
To displace the atoms along a set of random or a single specially chosen direction [2], this approach requires the knowledge of the phonons on a supercell. The displacement length is determined by the temperature of the ionic system. The bandgap can be directly obtained by averaging over the set of randomly displaced supercells, or from the aforementioned special displacement pattern.
Many-body perturbation theory
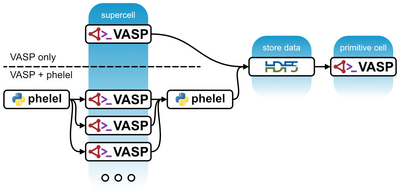
Another approach to include electron-phonon coupling employs the methods and language of many-body perturbation theory, where the coupling is included as a perturbation of the electronic or phononic states. In the case of the perturbation of the electronic states, we can access the bandgap renormalization as well as electronic transport coefficients with the inclusion of phonon scattering.
This approach entails computing the electron-phonon matrix element and the phonon-induced electron self-energy. Within the framework of density-functional theory this requires the knowledge of the change of Kohn-Sham potential with an ionic perturbation as well as the initial and final electronic Kohn-Sham states. The calculation is done in two steps:
Step 1: Electron-phonon potential from supercells
- In the first step, we obtain the derivatives of the Kohn-sham potential with respect to the ionic displacements
- with the ion index and denoting the Cartesian direction in which it is displaced. The main output file is phelel_params.hdf5, which is required for computing the matrix elements in the next step.
- How to compute the electron-phonon potential from supercells
Step 2: Physical observables (or electron-phonon matrix elements)
- To compute the physical observables, the phonon-induced electron self-energy is computed in the primitive cell. The main tag that provides convenient defaults depending on the observable of interest is ELPH_MODE. The computation of the self-energy requires evaluating the electron-phonon matrix elements
- By default, we avoid writing the matrix elements, because it is a huge data set which is distributed for optimal use of the computational resources.
- For details on the setup and practical advice, we recommend reading
- Bandgap renormalization due to electron-phonon coupling
- Transport coefficients including electron-phonon scattering
- See the ELPH_DRIVER tag to obtain the electron-phonon matrix elements for further post-processing.
References
Pages in category "Electron-phonon interactions"
The following 55 pages are in this category, out of 55 total.
E
- Electron-phonon interactions from Monte-Carlo sampling
- Electron-phonon interactions theory
- Electron-phonon potential from supercells
- ELPH DECOMPOSE
- ELPH DRIVER
- ELPH IGNORE IMAG PHONONS
- ELPH ISMEAR
- ELPH KSPACING
- ELPH LR
- ELPH MODE
- ELPH NBANDS
- ELPH NBANDS SUM
- ELPH POT FFT MESH
- ELPH POT GENERATE
- ELPH POT LATTICE
- ELPH PREPARE
- ELPH RUN
- ELPH SCATTERING APPROX
- ELPH SELFEN BAND START
- ELPH SELFEN BAND STOP
- ELPH SELFEN CARRIER DEN
- ELPH SELFEN CARRIER PER CELL
- ELPH SELFEN DELTA
- ELPH SELFEN DW
- ELPH SELFEN FAN
- ELPH SELFEN GAPS
- ELPH SELFEN IKPT
- ELPH SELFEN KPTS
- ELPH SELFEN MU
- ELPH SELFEN NW
- ELPH SELFEN STATIC
- ELPH SELFEN TEMPS
- ELPH SELFEN WRANGE
- ELPH TRANSPORT
- ELPH TRANSPORT DFERMI TOL
- ELPH TRANSPORT DRIVER
- ELPH TRANSPORT EMAX
- ELPH TRANSPORT EMIN
- ELPH USEBLAS
- ENCUTLR
